Perspective

You’ve probably seen this before, maybe you’re one of today’s lucky 10000.

What’s the number of the covered parking spot in this image?

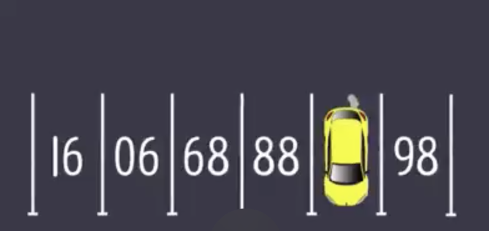
When I first saw this I had no idea. Eventually I decided it had to be 128. Because pairwise, 16 - 6 = 10, 68 - 88 = -20, so x - 98 = 30. That’s a stretch, but it made some sense.

Of course, for parking spot numbers that makes no sense. Who would number parking spots like that? You’d never find your parking spot, and there would be duplicates. Really bad idea.

On the other hand, it’s all a matter of perspective. If you look at it this way, it seems pretty obvious.

In this case it’s clearly 87. And that makes sense from a real-world parking lot perspective as well.

So what do we learn from this? We learn that our perspective, our biases, can change how we solve problems. 

Back in my aerial imagery days we had to deal with lens distortion. We needed to minimize it to get the most accurate images possible. Lots of effort went into multi-part lens design and construction. Managing thermal deformation, both during lens grinding and after installation was important. Things had to be just right. And we still couldn’t get rid of the distortion.

So we cheated. Or rather we looked at the problem from the other direction. Given a perfect test image, in our case a grid of points, and an actual image, what kind of post-capture transformation did we need to do, at the pixel level, to get the correct image. We couldn’t calculate it before hand, but we could easily measure the deltas. So we did. Then we inverted the direction. And then we applied them to all of the raw images. Which removed (almost) all of the distortion.

So what are currently you doing at one end of a pipeline that you could do more easily at the other?